First steps

Taking on a full 3-5 lesson project is a big initial step. Alternatively, each of the Professional Development modules incorporates two or three sample tasks and suggested lesson plans, which have similar themes to the case studies but are designed to be completed in a single lesson. You can view the PD materials to see how teachers have incorporated these tasks into lessons and how they and their pupils got on. Likewise the stand-alone assessment tasks can be completed in 20 minutes to an hour, and might provide a starting point before you commit to a multi-lesson case study.

Problem types and practicalities

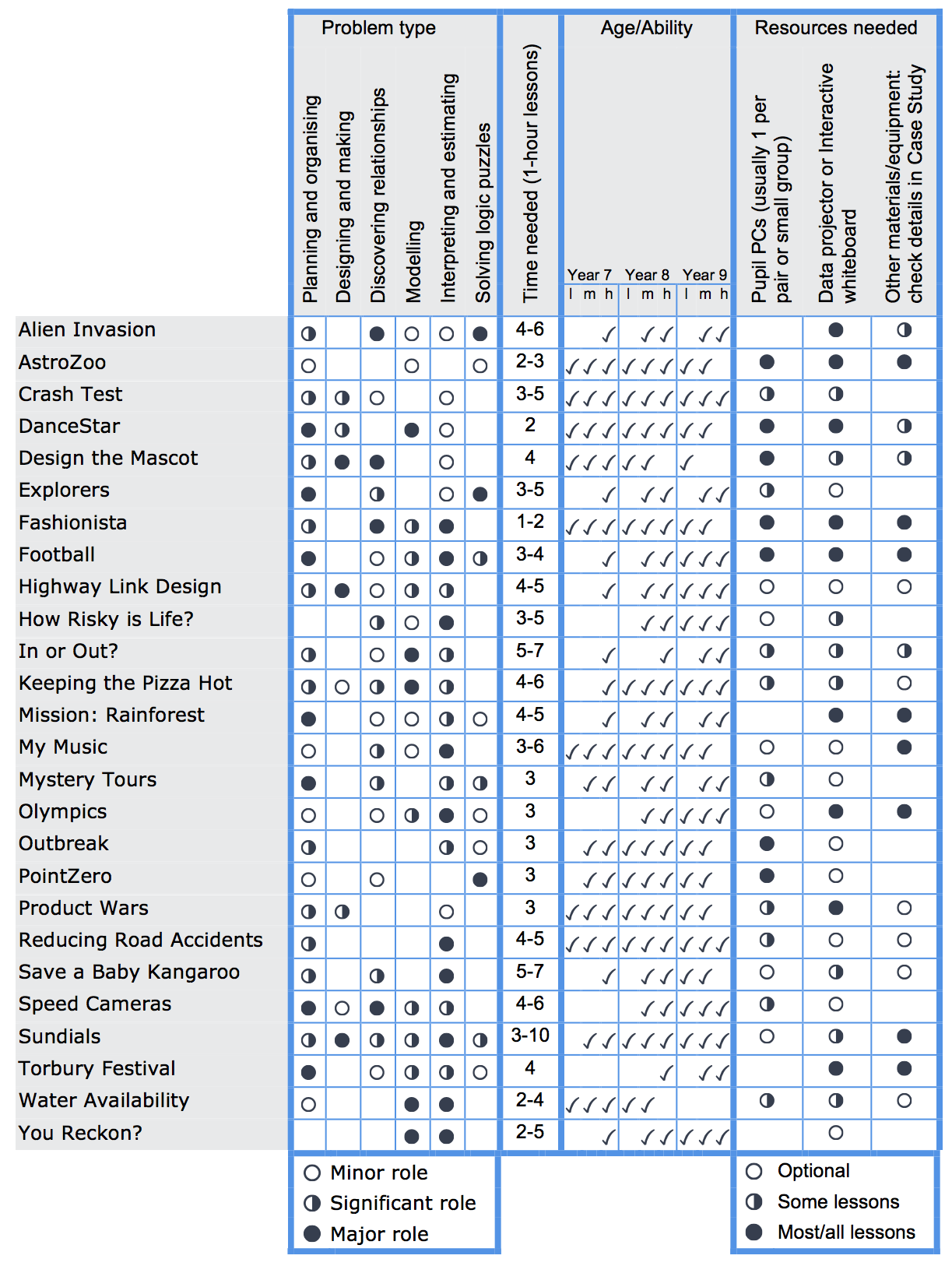
This comparison chart shows the general types of problem encountered in the Case Study projects, the suitability for age and ability groups and other practical considerations, like extra resources needed.

Type of problem

The projects cover six broad types of problem – planning and organizing; designing and making; modelling and explaining; exploring and discovering relationships; interpreting and explaining; solving logic puzzles. A case study may have more than one of these aspects.

Time required

The number of (typically) 1 hour lessons suggested to cover the material

Suitability for age and ability groups

In terms of low, medium and high ability in UK school years 7-9 (ages 11, 12, 13)

Resources needed

Some Case Studies need computers or an interactive whiteboard for all or part of the project – a few case studies require other resources

Content areas, concepts and processes

One aim of the Bowland materials is to encourage pupils to choose, combine and apply mathematical tools from across the curriculum. Consequently, each project typically covers a range of mathematical topics, and a particular topic may only form a small, or optional part of a project, so sorting the projects by specific mathematical topic is not particularly useful. The table below summarises the content in terms of the three main curriculum areas of Number, Geometry and Statistics.

The table also shows the Key Concepts, Key Processes and Curriculum Opportunities from the 2008 English National Curriculum. While this language is not part of the 2014 curriculum, the framework is still useful for analysing the problem solving and mathematical thinking skills requirements of the new curriculum.

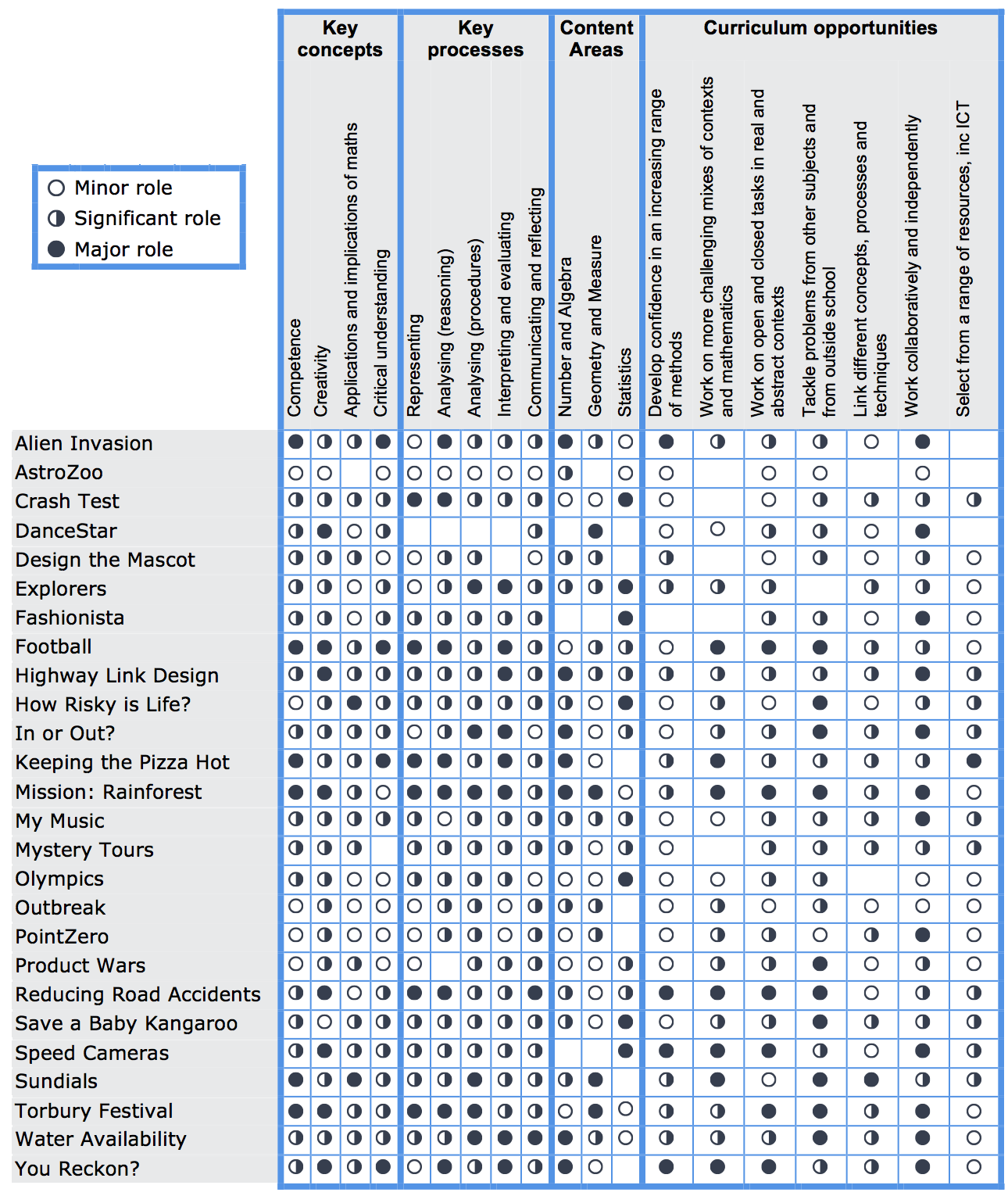
Note: These charts are intended to indicate the coverage of each Case Study and are not an assessment of relative "quality". They reflect the diverse nature of the Case Studies: some focus on a specific topic or activity type while others cover a wider domain. Please check the individual case study documents for detailed ICT and other resource requirements well in advance of the lesson – the chart above is just a general guide.

Examples of mathematical activities

This summarises the specific mathematical activities involved in some of the case studies

Alien Invasion

Locate spaceships using clues to estimate and calculate distances and directions. Interpret graphs and maps to plan an escape; crack a code to escape from a cell. General problem solving.

AstroZoo

Solve problems associated with keeping creatures in a closed environment – oxygen supply, heat, power – using proportional reasoning and linear relationships.

Crash Test

Control variables systematically (e.g. speeds, design of cars, barrier types). Make hypotheses and test them by observing the effects in crash test experiments. Present findings to the class.

DanceStar

Devise notations to describe the moves in various styles of dance.

Design the Mascot

Design a toy character for a 60 by 80 pixel display. Scale proportionately for different types of display. Conduct market research into the design.

Explorers

Plan a route in space, bearing in mind fuel, food reserves and distance. Trade between planets using fantasy units of currency. Use algebraic functions to decide where explosive charges should be placed to destroy asteroids.

Fashionista

Use charts and graphs to analyse buying patterns in a ficticious shop. Combine these with population data to predict sales and plan stock buying.

Football

Analyse players’ performances on various training exercisies to select a team. Explore the geometry and timing of passing a football. Investigate the probabilityof scoring with penalty shot aimed at different parts of the goal.

Highway Link Design

Propose the location of a by-pass, using data tables and graphs from the Highways Agency. Find ways to satisfy constraints (minimum radii of curvature, verge clearance, cambers etc). Cost and present proposed solutions.

How Risky is Life?

Compare perceptions of the causes of death with actual statistics. Interpret very large and very small probabilities. Decide what these say about behaviour and attitudes. Explore random variation.

In or Out?

Use photographic and slow motion evidence to decide qualitatively, then quantitatively, whether a batsman (in cricket) is ‘in’ or ‘out’. Select variables, make estimates of distances, times and speeds and use algebraic models.

Keeping the Pizza Hot

Choose packaging for a pizza. Measure temperatures as the pizza cools. Use data logging software. Fit a graphical model to the cooling of a pizza. Calculate the longest reasonable travel time before a pizza becomes too cold to eat.

Mission: Rainforest

Choose a camp location on a map using unit conversion, estimation, volume and surface area calculations and co-ordinate geometry. Apply multiple mathematical techniques to make plausible estimates about the effects of deforestation.

My Music

Describe the characteristics of individual genres of music. Use the tempo of music and other variables to illustrate compound measures, eg beats per minute.

Mystery Tours

Plan a 5-day trip to satisfy money/time constraints and to keep happy three sets of tourists with different requirements. Convert currencies, satisfy baggage allowances etc.

Olympics

Interpret the records of men’s and women’s athletics performance over the years to decide if women are set to out-perform men in the future.

Outbreak

Use coordinate clues to locate infected people. Mix ingredients in proportions to create an antidote. Use resources optimally to design a vaccination programme.

PointZero

Solve number, spatial and logic puzzles to progress in an escape adventure game. Use number sequences to escape from a building. Use rotation and reflection to recreate a given pattern. Use codes and loci to escape from underground tunnels.

Product Wars

Design a questionnaire and conduct market research for a new drink. Mix ingredients to obtain nutritional value and taste; design packaging for the drink.

Reducing Road Accidents

Explore a town’s accident database. Control variables to decide on the most effective allocation of a sum of money to provide safety measures. Prepare a case and present it.

Save a Baby Kangaroo

Determine the age and species of a ‘Joey’ from tail and foot measurements and graphs of growth data. Devise an appropriate nutrition regime from tables of nutrient data. Present and justify this regime.

Speed Cameras

Explore perceptions of randomness and relate this to the perceived effectiveness of speed cameras. Simulate the effects of different sitings.

Sundials

Design, examining the maths, and then construct a sundial, using symmetry, angles, nets, origami, graphs and charts.

Torbury Festival

Plan how to drain a flooded site using areas, volumes and rates of change. Plan the stock for a stall, considering profit margins and limited space. Choose the optimum position for lookout towers using geometry, such as similar triangles.

Water Availability

Analyse a complex decision faced by a water aid agency. Devise and use a compound measure (eg per capita) to decide on a 'fair' distribution of resources.

You Reckon?

Break a problem into its component parts; combine everyday knowledge to create chains of reasoning that result in reasonable estimates of useful quantities.